Complexity theory

Complexity theory reiterates on concepts from satisfiability and NP-completeness.

NP

We define a decision problem as a problem where given an input $I$, we output either True or False depending on if there exists a solution matching the problem’s requirements.

Suppose that we have a witness $W$ — some entity that can observe the decision problem running and see a solution that the decision problem uses to output True. With this, we can divide decision problems into two classes:

Verifiable decision problems. We can verify the solution given from $W$ in polynomial time relative to $I$.

Hard verifiable decision problems: There is no known polynomial time verification to the solution from $W$; our current understanding tells us that we need exponential time for verification.

We denote $\mathsf{NP}$ as the class of all verifiable decision problems. We could also define $\mathsf{NP}$ as the set of all search problems, where a search problem meets these conditions: (1) for an input $I$, its algorithm outputs a solution $S$ or specifies that there is no solution, and (2) for a candidate solution $S$, it is possible to verify its correctness in polynomial time relative to the size of $I$.

MST Decision Problem

Given input $I:G(V,E),r$, output whether there exists a spanning tree of $G$ with weight $\le r$. 2. Verify that ${\sum }_{e\in s}w(e)\le r$, where $w(e)$ is the weight of edge $e$.

Summing all the runtimes, we get $O(|V|+|E|)$, which is polynomial time. MST is in $\mathsf{NP}$.

K-coloring

Given input $I:G(V,E)$ and $k\in \mathbb{N}$, output whether there exists a $k$-coloring of $G$. A $k$-coloring is an assignment $\sigma$ for all $v\in V$ such that $\forall e=(u,v)\in E,\sigma (u)\ne \sigma (v)$.

Suppose we find a candidate assignment $S$. Then, we could iterate through each edge $(u,v)$ in $G$ and check that $\sigma (u)\ne \sigma (v)$. This takes $O(|E|)$ time, so $k$-coloring is in $\mathsf{NP}$.

0/1 Knapsack

Given input $I$, a set of items $\mathrm{1..}n$ with corresponding values $v_1..v_n$ and weights $w_1..w_n$, and a capacity $B$, output whether there exists a collection of items that maximizes the total value and keeps total weight $\le B$.

Suppose we find a candidate collection $S$. We can easily show that the total weight $\le B$, but we will need to run Knapsack-search to find if the total value is maximized. However, Knapsack-search runs in pseudo-polynomial time, which is really exponential time. The runtime of Knapsack-search is $O(nB)$, but since it takes $lo{g}_2(B)$ bits as the input size to represent $B$, the runtime is $O(n{2}^{lo{g}_{2}B})$, which is exponential with respect to $I$. We hence cannot conclude that 0/1 Knapsack is in $\mathsf{NP}$.

SAT

Given a function $f:x_1..x_2\to 0,1$ in conjunctive normal form (CNF), output whether there exists an assignment $x_1..x_n$ such that $f=1$.

Suppose we have a function $f$ in CNF: $(x1\vee x2\vee x3\vee x4)\wedge (\bar{x}1\vee \bar{x}4\vee x5\vee x6)\wedge (x3\vee \bar{x}5\vee x7)$ and a candidate assignment $S:x\mathrm{1..}x7$. To verify $S$, we just have to plug $S$ into $f$. This takes $O(nm)$ time, where $n$ is the number of literals and $m$ is the number of clauses.

The subset of $\mathsf{NP}$ problems where we know of a solution that solves the problem in polynomial time is $\mathsf{P}$. We have that $\mathsf{P}\subseteq \mathsf{NP}$. For example, MST is in $\mathsf{P}$ because of Kruskal’s and Prim’s.

Reductions

A reduction from problem $A$ to problem $B$ shows that $B$ is at least as hard of a problem to solve as $A$. We take an input, or instance $I$ in problem $A$ and convert it to an input $I^{\prime }$ of problem $B$ using a polynomial time function $f$. Then, we retrieve a solution $S^{\prime }$ by running any algorithm for $B$, and then convert it back to a solution $S$ of $A$ using a polynomial time algorithm $h$.

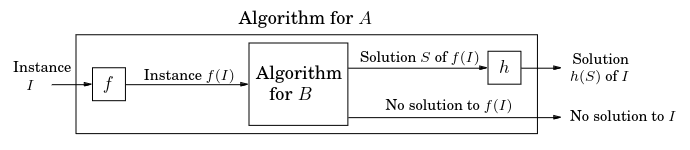
To complete the reduction, we must show that there is a solution to input $I$ for $A$ iff there is a solution to input $I^{\prime }$ for $B$. We show that $A$ is just a special case of $B$, therefore $B$ must be at least as hard as $A$. This process involves three steps:

1. Describe the function $f$, which is the transformation of the instance $I$ for problem $A$ to instance $f(I)=I^{\prime }$ for problem $B$, and show that it runs in polynomial time.
2. Describe the function $h$, which converts the solution to instance $I^{\prime }$ from $B$ back into a solution for instance $I$ in $A$.
3. Show that there is a solution for $I$ in $A$ iff there is a solution for $I^{\prime }$ in $B$. To prove that $a\leftrightarrow b$, you must show that $a\to b$ and $b\to a$. It is often easier to use the contrapositive and show that $a\to b$ and $\neg a\to \neg b$. It doesn’t need to be a rigorous formal proof, just show correspondence in both directions.

A problem $C$ is NP-hard if there exists a reduction $A{\le }_{p}C$ from all problems $A\in \mathsf{NP}$. Therefore, $C$ is at least as hard as all problems in $\mathsf{NP}$. Therefore, you can prove a problem $D$ is NP-hard by finding a reduction $H{\le }_{p}D$ for some known NP-hard problem $H$.

A problem $C$ is NP-complete if it is in $\mathsf{NP}$ and NP-hard. NP-complete problems are the hardest known problems in $\mathsf{NP}$, as all other $\mathsf{NP}$ problems reduce to it.